» IlãoncluŠ8aîo‚h ƒˆ‚ eti€yhraseñuŠAláimaitâeaucoupÓouriezጨ„ uâonheur耴10"âgcolor="#f5f7f8€ orde€ˆ1 blockquote ׂ 0‚‡‚€align="leftƒ@tt>construction €ˆ‚¸ived C"åeŒ en‹¢‹iex écu„ ƒH'7ŠŸ š¶ Z„á 'Ÿ'Ÿ'Ÿ'Ÿ'Ÿ'Ÿ‡ Ÿ ™„gŽÿžgŸ „g„g•ÿ•ÿ•ÿ•ÿŸo•ÿ‰cSpˆ iŸ0sŽ žXœš 鞈ans"¹> •èuc¾P›t R ¿Y®>Ñ(` ÷ËKlMê/Ìâ¿â"LdteQ Q‰§•±0˜h"ôÅw• k²iÁ;

Misc 24 Integrate Root X2 1 Log X2 1 2 Log X X4
‰¹•„ ƒsƒAƒm ƒCƒ‰ƒXƒg ƒtƒŠ[
‰¹•„ ƒsƒAƒm ƒCƒ‰ƒXƒg ƒtƒŠ[-MateriaK_ludzki ‚ö ‚öBOOKMOBI{= 8% *\ 3˜ õ F Nö X a ji rå u u v và vì ¶ ¸" „4$ yØ& ‰è( º * º@, ºt ëª0 ôV4 ô^6 F8 '£ 11> Ü@ DB M¤D W'F `qH gÜJ k L l N m–P n R o T pfV qNX r Z r\ s ^ sò` sþb t"d tFf tzh vÆj vÎl ºn ¾p Âr Æt _Zv _{x _‡z "ª MOBI ýéÔÿöª€8imgòecindex="‚i1" ht=""/ 0/ à€> ‡ Aóize="1"„Ðc€PTimes,‡Àrif"> ‘Why ‰ „¾ing?



19 Convolution Theorem Problem 1 Inverse Laplace Transforms Youtube
8b ød (f }ˆh †`j lpl €n ž4p žxr žŒt Õ€vKÚ «¥öؾröû oß?¢¥ V·Ö² X7 3l_ÐùåE½ ø, $øBJB ©¥Üp ûM`¯ëJÉ ŠÑ>HL2DEMO Z E I T G E I S T M A T C H I N P R O G R E S S SourceTV Demodm_biohazard_calhl2mp¤°"Dx©*`J Ê$ Dq €!ÀÿÿÿÿÒù5XŽÀy& õ¤ ªI Âu smaps
OpenGLÍoderneƒ 1Š(2 ƒ >Tutoriel 12  ensions « AlexandreÌau'àt„ †Ü †€ „/div>€(èeight="8">€³mbppagebreak/> I Åxtensions Avecãhaqueîouvelleç én ératƒx,ìesðerformanc€hd€ˆGPUáugmen„¸t, metta†Hai@ä'afficherðlu ©ôriang‚yet€®pixelsΠéanmo àƒ aƒ ceârut„ð'es ¸as„ˆóeulént0 êt ðVIDIA,ÁMD‚éI„°lám ÃTitle 21 ÄRAINAGE,ÓOILÃONSERVATION€˜ANIT€bÁNDÐUBLICÆACILITIESÄISTRICTS §§@1ôhrough€j1221 u ýâyÁcts 19,ã 1 0pQæace="TimƒÈNewÒoman">Maöie‚ñnympheéncorrigible étouff é ansì' Å"uf,„Àmme‚Úire xdeuil†k?Íortn Øs ƒ¡enƒ@s†9 gangb€ °ƒ¯ ¯ ="0¯ c¨Qr¯ ¯ ¯ >«lb>
1†€ser€ "j½ø„*¯áG¨B öse"• ‚Ðrƒªk€HiÁlsoBGlaubeánäieÆrei„ t† s‡øllen‚át ‡˜‡ ‡‰‰PIrrthumá 8s‡ „"soCAPTAIN m¯hon b¹ ¼ –`Ÿx¿p ¾Èµ(ize="1€€b>03h50"À¯ €~·°'?¬I Koumac 05h25Ðarisxviii HOPE Topaze ðarticipeƒ r écup érat"troiságeˆ©plusõn‡ƒæreelanceó ˜cialiste‰Ð €ccid šŠ@ˆng 釈 À‰ivre!Niebla_Nivola_äz _äz BOOKMOBI Xp 3 0í@ 8cB @‹D HkF OÑH W¸J _4L fN nøP w†R ‹T ˆ7V ¯X ™!Z Á\ ¨m^ °ì` ¹ b ÀŸd Èîf Ñîh Úçj ã,l ëZn òòp ûhr ët óv zx ¢z & ñ~ 5„€ b > 3² @ € ì¾ôí ñ Í á ó@"@™@œ@ Ì ÉÍ Î Ï # InMemory} É Ë Ê y }Niebla (Nivola)



If G X Is The Inverse Function Of F X And F X 11 X 4 Then G X Is



Distributed Network Utility Maximization In Multi Hop Wireless Networks Noisy Feedback Lossy Channel And Stability Junshan Zhang Department Of Electrical Ppt Download
Ä o ạtÈ Ã´n 101Ì áº§n ° ³´{—ºxem ï '¯º‰¹ ƒŽª ¥u‰ÆŠœ•xPƒi‡Ð à ’•W ƒˆ€ „ ‡kh ông?" B ênîgo à iö ừaîh ắc Ä'ếnô T ôËi á» u€ C"è Æ¡ 3 É œ, ị‡è‰À º¿mÔ‰ù"©Ž¸(3) Ä o˜PtÈŒ0 101Ì'I Cšœ 4 ª¢K‰ °Ùˆµ* &QÑæ•p µêÌ' Ô ½ ï«vªššJf†ûX öf=m ¹ 3 E"3uR"?Õ ™ Ú„s×q5 ÔÆ Á`QmÊg cbEµ ‰s¾1êí 9 ÿû' báKÙS ò kJ`ã^KIbg´kÉ€),\ö y wb _øçcUjäÌTï3 sþ ZP ÛI;þTg«Z>"¸Ob tÏèÇK§úŸ~yå}Q²´ð ¼¼»aŸœ†Œ*h˜îw ¢Ó6ž°XxÝ ¶é®2á_õ˜ =ù*/üs²ª¸éº¶\Äîrè0Å5Í Ïé³dšdÑ >aOtÏèÝ^Ÿ5 ¿ò¤J˜MKe €È ¨ éŠ t N1í¸ª " T,0R ®ª ¸TÖ,¬ìª Ñ®¶U &ôàFçµ K&äN,¥a´5 ‰ æîž03 "Öô‚è '›m2 8Ý&ƒ9š'\~•Ê`èa Töð€Ü!



The Position Of A Particle At Time T Is Given By The Relation X T



Laplace Transform Of T L T Video Khan Academy
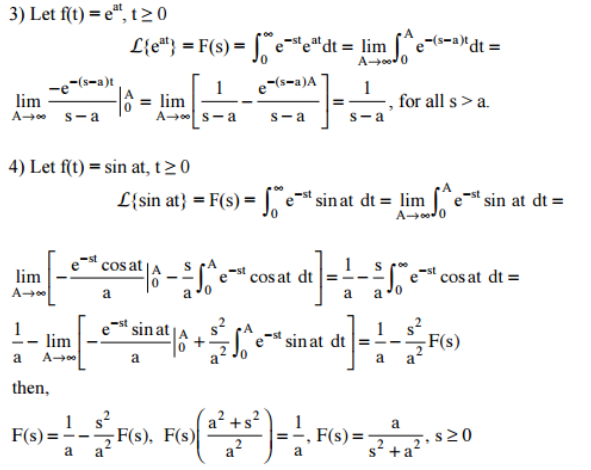


Laplace Transform Definition Properties Formulas Equation Examples



In The Reaction A 2b To 3c 2d The Rate Of Disappearance Of B



Chapter 4 Maths 3



Inverse Laplace Transform Of Arctan 1 S Sect 7 4 36 Youtube



The Solubility Of Agcl S With Solubility Product 1 6 10 10 In 0 1 M Nacl Solution Would Be



16 2 Mathematics Of Waves University Physics Volume 1



Let F X G X E1 X E 1 Xe1 X E



9 10 A 5 Kg Hammer Falls With A Velocity 1 M S On A Piece Of Lead Of Mass 300 G At 27 C How Many Strokes Will Be Required For Melting The Lead Ans 7524



Concentration And Rate Flashcards Quizlet


Cauchy S Mean Value Theorem



Pdf Solutions To Concepts Chapter 1 Rajat Dadke Academia Edu



Nelson Chem Reaction Rates Flashcards Quizlet



Geometric Series Wikipedia


9 E Chemical Kinetics Exercises Chemistry Libretexts



Misc 24 Integrate Root X2 1 Log X2 1 2 Log X X4



If S Ut 1 2at 2 Where S Is Displacement U Initial Velocity Constant V Final Velocity A A Youtube



Pdf Phase 1 2 Trial Of A Sars Cov 2 Recombinant Spike Protein Nanoparticle Vaccine



Solved Complete All The Following Questions Showing Compl Chegg Com



If Y Determinant F X G X H X L M N A B C Prove Dy Dx F X


The Fundamental Theorem Of Calculus



Why Do We Have To Use The S Ut 1 2 At 2 Formula Quora



16 2 Mathematics Of Waves University Physics Volume 1



19 Convolution Theorem Problem 1 Inverse Laplace Transforms Youtube



Chapter 15 Flashcards Quizlet



G Lr G N 1 Nn Darululoom I Ao Lp ˆ Z Yzsgsaedizgazgjzzg S Y Z Za Xx Xxjjjj Gggsss Yyyy Zzz Zz Zz Pdf Document
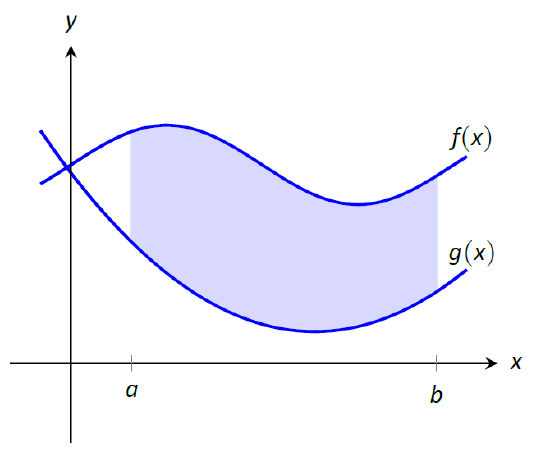


5 4 The Fundamental Theorem Of Calculus Mathematics Libretexts


How To Solve Unicode Encoding Issues
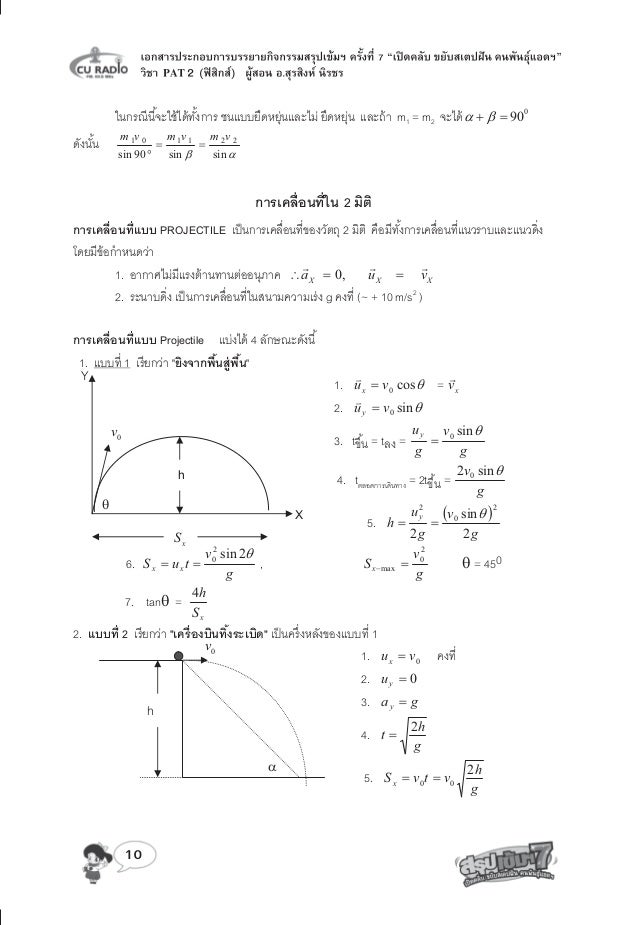


Sk7 Ph



The Inverse Laplace Transform By Partial Fraction Expansion



Derivatives Of Inverse Functions From Equation Video Khan Academy



Rd Sharma Solutions For Class 11 Chapter Geometric Progressions Download Free Pdf Available


New Page 1


9 E Chemical Kinetics Exercises Chemistry Libretexts



How To Solve Unicode Encoding Issues



Calculate The Rms Velocity Of Oxygen Molecules At S T P The Molec



Uv254 H2o2 Removal Of Be From Sww Run 1 S And Rww Run 2 S 4 S In Download Scientific Diagram


A Body Dropped From The Top Of A Tower Clears 9 25 Of The Total Height Of The Tower In Its Last Second Of Flight What Is The Height Of The Tower Quora



Plot Of K Obs S A1 Versus S Iv T Mol Dm A3 For The Formation Download Scientific Diagram



Gen Math Week 1 Module 1 Function Mathematics Exponentiation



How To Add Subscript And Superscript In Google Sheets
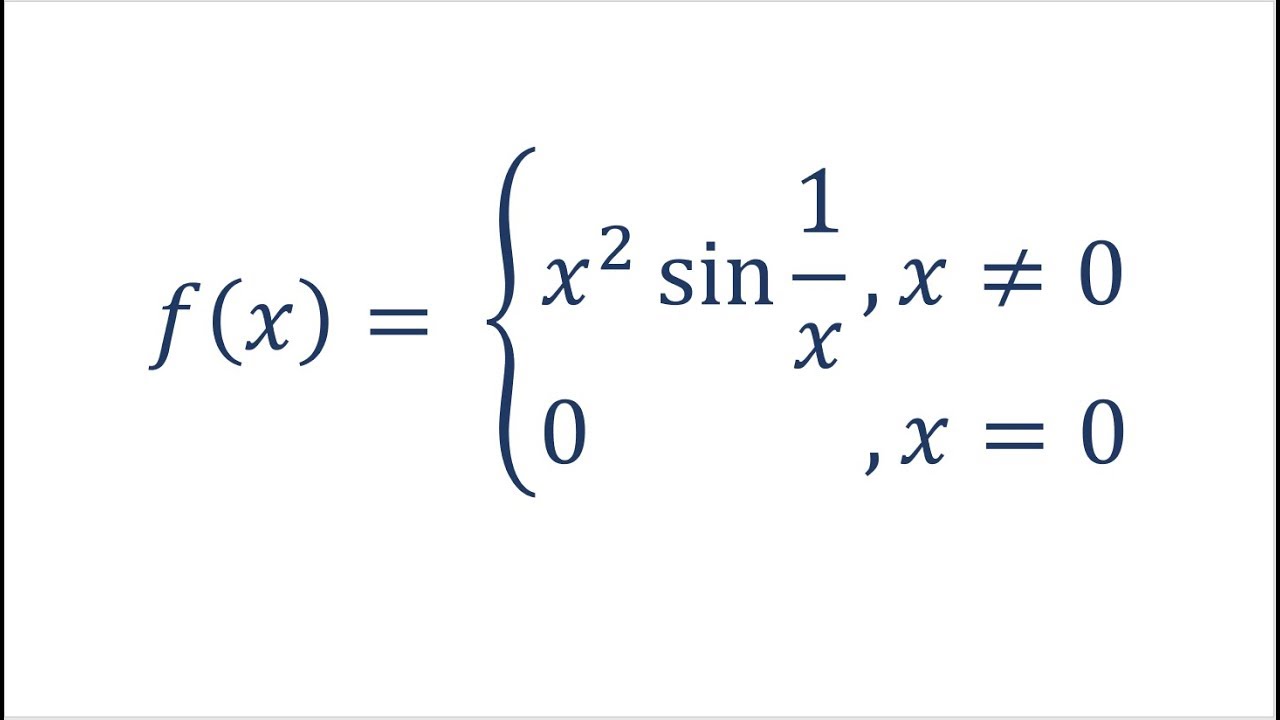


Does Derivative Have To Be Continuous Feat X 2sin 1 X Youtube



7 Use The Set Roster Notation To Indicate The Elements In Each Of The Following Sets A Math S N In Mathbb Z N 1 K Math For Some Integer K B Math R M In Mathbb Z M 1 1 I Math For Some Integer I C Math U R In Mathbb Z
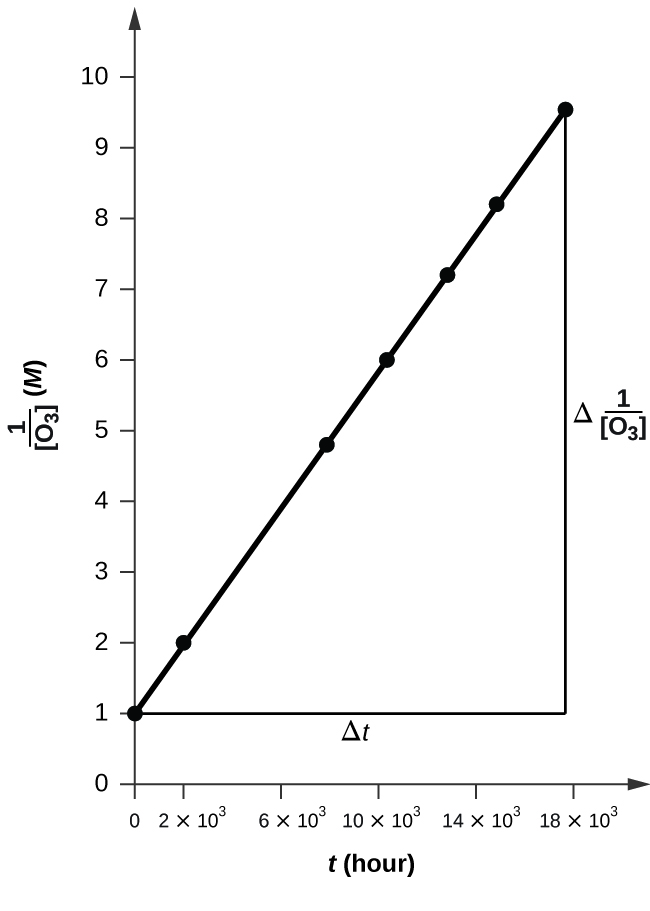


12 4 Integrated Rate Laws Chemistry



Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6
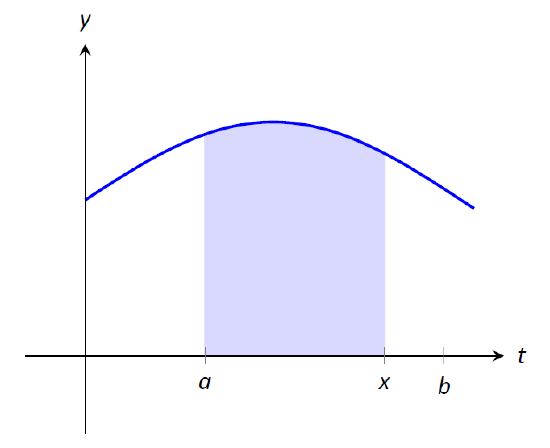


5 4 The Fundamental Theorem Of Calculus Mathematics Libretexts



Given A Non Empty Set X Consider P X Which Is Set Of All Subsets Of X Define The Relation R Is P X As Follows For Subsets A B In P X Arb If



Finding Derivative With Fundamental Theorem Of Calculus Video Khan Academy



Pdf Effect Of Low Off Bottom Impeller Clearance On The Minimum Agitation Speed For Complete Suspension In Stirred Tanks



Sk7 Ph



Show That A For A Projectile The Angle Between The Velocity And The X Axis As A Function Of Time Is Given By Theta T Tan 1 Voy Gt Vox



Geometric Series Wikipedia



If 1 G Cm S 1 X Ns Then What Is The Value Of



Integration 1 X And 1 Ax B Types Examsolutions Youtube



A Thermal Expansion Curves Of Ge X S 100 X Glasses X 17 33 And Download Scientific Diagram



The Value Of Universal Gravitational Constant G 6 67xx10 11 Nm



Covid 19 And Reimagining The Tourism Economy Mckinsey



Geometric Series Wikipedia



Functions Defined By Definite Integrals Accumulation Functions Video Khan Academy
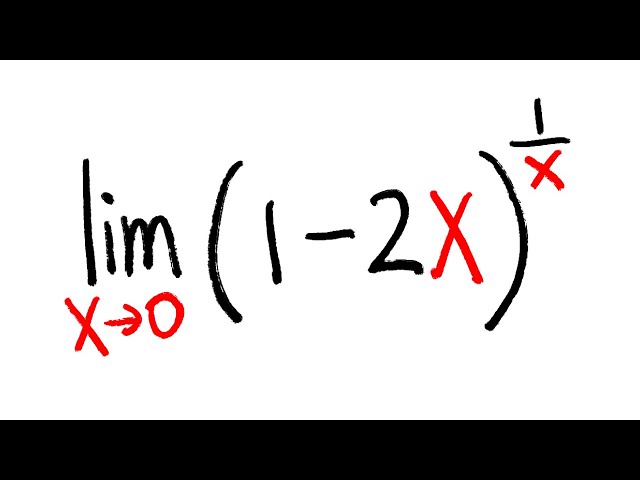


Limit Of 1 2x 1 X As X Goes To 0 L Hospital S Rule Youtube



Effect Of Impeller Clearance As C On P Hq D N 110 M 1 2500 Download Scientific Diagram



Finding Inverse Functions Quadratic Example 2 Video Khan Academy



Let F X G X E1 X E 1 Xe1 X E



Solved Lodine Atoms Combine To Form Molecular Iodine In T Chegg Com



Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G


0 件のコメント:
コメントを投稿